新潮文庫の「和算の侍」という、江戸時代の和算をテーマにした短編小説集を読みました。鳴海風(なるみふう)さんの著作です。
鳴海風さんは、1953年生れの65歳です。新潟県に生まれて東北大学機械工学科で修士を取得してデンソーに入社しました。エンジニアとして働きながら、小説家を目指し、40歳を前にして「円周率を計算した男」で歴史文学賞を受賞して、小説家としてデビューしました。
その後も二刀流を続けながら、和算をテーマにした作品を中心に多くの著作があります。2013年に60歳の定年でデンソーを卒業しました。現在は、小説家として、和算の研究者として、執筆や講演に忙しくされているそうです。
ちなみに、デンソーの同じ部署に3年遅れて大阪府立大学電気工学科から入社したのが、東野圭吾さんだったそうです。東野さんは入社4年目に「放課後」で江戸川乱歩賞を受賞して、すぐに小説家デビューしています。
さて、「円周率を計算した男」とは江戸時代の算術家、建部賢弘のことです。
古今東西、世界中の人が円周率を求めようとしていました。円周率は果てしなく続く無理数です。建部の時代の世界記録は、オランダのコーレンが計算した35桁だったそうです。
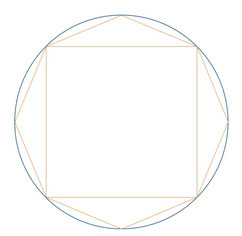
どうやって円周率を求めるかというと、先ず円に内接した正方形の周長を求めます。次に、正方形と円の間に正八角形を内接させて周長を求めます。これを繰り返していけば、円に近似させることができるわけです。コーレンは正2の62乗角形まで計算して、円周率を35桁まで導きました。
建部はコーレンとは違う効率的な方法で、正1024角形までの計算で円周率を41桁まで正確に求めています。しかし、その後には、この力任せのやり方から離れて、極めて精度の高い近似法を見い出しました。今から300年近く前の西暦1722年(享保7年)のことです。
それが、建部の公式です。円周率をnと置くと、
n^2/9 =1+12/(3*4)+12*22/(3*4*5*6)+12*22*32/(3*4*5*6*7*8)+ …
という式で表されるものです。
n^2/9 =1 なら n=3
n^2/9 =1+12/(3*4) なら n=3.122・・・・
n^2/9 =1+12/(3*4)+12*22/(3*4*5*6) なら n=3.1384・・・・
どんどん円周率の真の値に近づいていきます。
江戸時代に鎖国政策の日本で、西洋世界とは全く隔絶したなかで、多くの数学者が切磋琢磨していました。そして、世界的に卓越した優れた数学の業績が数多く成されたことは驚愕です。
スイス人のオイラーが建部の公式にたどり着いたのは、15年後のことでした。
