ギリシア時代から多くの数学者を悩ませていた3大問題が解決したのは19世紀後半でした。
古代ギリシアの数学界で関心を集めていた3大作図問題というものがあります。
①任意の角の三等分を作図する。
②与えられた立方体の二倍の体積を持つ立方体を作図する。
③任意の円と等積の正方形を作図する。
この問題は2000年以上解決されないままになっていました。
例えば、①の「任意の角の3等分」ですが、直角(90°)なら下のように簡単です。
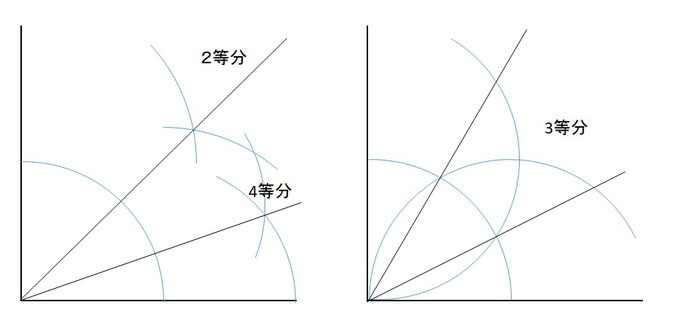
二等分は小学校で習います。四等分は二等分を2回繰り返すと描けます。
三等分は円弧を引いて、直線との交点から同じ半径で円弧を引きます。円弧の交点と原点を結ぶと三等分線です。
直角ならば簡単な三等分ですが、任意の角では描くことができません。
任意の角θの三等分の作図は、(cos1/3θ,sin1/3θ)が作図可能であるかという問題に帰着できます。
cosの三倍角公式より、
cosθ=4cos^3(1/3θ)ー3cos(1/3θ)
cos(1/3θ)=xとして変形すると
4x^3-3x-cosθ=0
となります。
cosθは任意の定数なのでxについての三次方程式の形になりました。
三次方程式の解の一般解には、三乗根が含まれています。
詳しい説明はできないのですが、
座標軸上の点が定規とコンパスのみで作図可能である条件は
① (x,y)成分がともに有理数である場合(わかりやすい)
もしくは
② (x,y)成分が有理数に√(平方根)を有限回使って表現できる数である場合
に限られるということが、代数学で証明されたのだそうです。
つまり、数値にnやeなどの超越数や三乗根が入ってしまうと作図できないわけで、任意の角の三等分線は引けないということが証明されたわけです。
同様に、ギリシャの3大作図問題は多くの人の頭を2000年間悩ませた末に、19世紀後半になって「できない」ということが証明されたということです。
これを、「下手な考え休むに似たり」と考えるべきではありませんね。
「幾何学的に考えると千年以上解決できなかった問題を、代数学という視点を使うことで解決することができた。」つまり、”異分野の考え方を導入することで、思わぬ新しい解決法が見つかることがあるという一つの例である。”と考えるべきでしょう。
最後に、現代のコンピューターが発達した世界では、ギリシャの3大問題は提起されない可能性が高いそうです。
三等分線をどうやって描くかを考える必要なんかなくて、二等分線を繰り返し描いていけば限りなく三等分線に近い(理論的には三等分線)線が描けるからという理由です。
1/3は,初項が1/4で公比も1/4の無限等比級数の和になります。
(1/3=1/4+1/16+1/64+1/256+・・・)
ちょっと味気ないですかね?
